Introduction to Hamilton-Jacobi-Bellman equations

Preface

这是一篇令人感到肝疼的文章，在ddl边缘疯狂徘徊的我通宵了两天肝出来的final project. 原paper是英文写的，简单翻译一下放到blog上，姑且算是最优控制论和HJB方程的入门.

感谢石老师提供的这个topic, 不然我当时就肝不完final project了. 然而我还是没学明白PDE，一学期下来就会个数值解hhh （丢人

Abstract

最优控制问题通常可以和非线性PDE——Hamilton-Jacobi-Bellman equations——联系起来. 在这种情况下我们可以关注HJB方程的解，这通常拥有很好的性质，而不是原来的问题. 在这片论文中，我们介绍了基本的最优控制论以及HJB方程的推导. 我们也证明了HJB方程的一些基本的性质. 一个高效的用于求解HJB方程的数值方法也在论文中被介绍. 最后，我们用HJB方程和其数值解解决了一个简单的现实中的最优控制问题.

Introduction of optimal control

最优控制论是微分方程的一个延申. 它主要讨论解决动力系统的方法，通常具有如下形式：

$$
\left\{
\begin{split}
& \dot{u}(t)=f(u(t),\alpha(t))\quad 0\leq t\leq T \\
& u(0)=u_0
\end{split}
\right.
$$

其中 $\alpha$ 成为一个"control". 现在我们能定义一个（需要被最小化的）cost functional

\[ J(\alpha)=\int_t^T l(u,\alpha)dt+g(u(T)) \]

其中 \(\lambda>0\) 为 discount factor. 因此，求解一个最优控制问题等价于求解一个最优问题：

\[ v(u,t)=\inf_{\alpha} J(\alpha) \]

我们称 \(v\) 为 value function. 在众多求出value function的方法中，其中一个是求解Hamilton-Jacobi-Bellman (HJB) 方程：

\[ \frac{\partial v(u,t)}{\partial t}+\max_{\alpha} \{ f(u,\alpha)\cdot Dv(u,t)+l(u,\alpha) \}=0 \]

伴随着terminal condition:

\[ v(u,T)=g(u(T)) \]

由于最优控制问题可以与这样的非线性PDE联系起来，我们可以关注HJB方程的解，而不是原始的ODE问题.

Basic property of HJB equation

首要的也是最重要的问题是“方程的解是不是的确是我们所需要的”. 如果我们假设value function是足够光滑的，我们可以宣称value function是HJB方程的一个解 [1].

Theorem: If \(v\in C^1\), then \(v\) 是HJB方程（伴随着terminal condition）的一个解.

Proof:

为了简化问题，我们用 $v(x,t)$ 代替 $v(u,t)$. 对于给定的 $h>0$, 选择一个常数control

$$ \alpha(s)=a $$

其中 $t\leq s\leq t+h$. 则从 $t$ 到 $t+h$ 的cost为:

$$ \int_t^{t+h} l(x,a)ds+v(x(t+h),t+h) $$

由于 $v(x,t)$ 是下确界, 我们有

$$
\begin{split}
& v(x,t)\leq \int_t^{t+h} l(x,a)ds+v(x(t+h),t+h) \\
\Rightarrow & \frac{v(x(t+h),t+h)-v(x,t)}{h}+\frac{1}{h}\int_t^{t+h}l(x,a)ds \geq 0 \\
\Rightarrow & v_t(x,t)+Dv(x,t)\cdot \dot{x}(t)+l(x,a)\geq 0\quad as\ h\to 0 \\
\Rightarrow & v_t(x,t)+Dv(x,t)\cdot f(x,a)+l(x,a)\geq 0
\end{split}
$$

由于不等式对任意control $a$ 成立，我们有

$$ \min_{a}{ v_t(x,t)+ f(x,a)\cdot Dv(x,t)+l(x,a) }\geq 0 $$

现在假设 $a^*$ 是对于上面的min的最优 control, i.e.

$$
\begin{split}
\min_{a}\{ v_t(x,t)+ & f(x,a)\cdot Dv(x,t)+l(x,a) \} \\
& = v_t(x,t)+ f(x,a^*)\cdot Dv(x,t)+l(x,a^*)
\end{split}
$$

则我们有

$$
\begin{split}
& \int_t^{t+h} l(x,a^*)ds +v(x(t+h),a^*(t+h))=v(x,t) \\
\Rightarrow & \frac{v(x(t+h),t+h)-v(x,t)}{h}+\frac{1}{h}\int_t^{t+h} l(x,a^*)ds =0 \\
\Rightarrow & v_t(x,t)+Dv(x,t)\cdot \dot{x}(t)+l(x,a^*)= 0\quad as\ h\to 0 \\
\Rightarrow & v_t(x,t)+Dv(x,t)\cdot f(x,a^*)+l(x,a*)= 0
\end{split}
$$

因此，value function是一个HJB方程的解.
□

然而，$C^1$ 条件过于强了. 在大部分情况下，HJB方程没有传统解，这意味着我们需要讨论弱解的存在性和唯一性. 有很多的工作表明由随机最优控制问题导出的HJB方程拥有唯一的velocity solution [2][3]. 重申原始的最优控制问题

$$ \left\{
\begin{aligned}
& \dot{x}(t)=f(x(t),\alpha(t))\quad 0\leq t\leq T \\
& x(0)=x_0
\end{aligned}
\right.
$$

我们将展示对应的HJB方程的弱解是唯一的.

Definition: HJB方程的弱解是一个函数 $v\in H^1$ s.t.

1. 对任意非负 $\varphi\in C_c^\infty$， 不等式对任意$\alpha$成立：

$$
\begin{aligned}
& \int_t^T (v(x,s),\partial_s \varphi(x,s))ds+(v(x,t),\varphi(x,t)) \\
& \leq (g(x),\varphi(x,T))+\int_t^T (l(x,s,\alpha),\varphi(x,s))ds \\
& +\int_t^T (v(x,s)\cdot Df(x,s),\varphi(x,s))ds
\end{aligned}
$$

2. 对任意非负 $\varphi\in C_c^\infty$ 以及任意给定的 $\varepsilon>0$, 存在 $\alpha'$ s.t.

$$
\begin{aligned}
& \int_t^T (v(x,s),\partial_s \varphi(x,s))ds+(v(x,t),\varphi(x,t))-\varepsilon \\
& \geq (g(x),\varphi(x,T))+\int_t^T (l(x,s,\alpha'),\varphi(x,s))ds \\
& +\int_t^T (v(x,s)\cdot Df(x,s),\varphi(x,s))ds
\end{aligned}
$$

Theorem: HJB方程的弱解是唯一的
Proof:
设 $v_1,v_2\in H^1$ 为弱解. 由[5]中的Lemma 4.5, 我们有

$$
\begin{aligned}
\int_t^T (v_2(x,s), & \partial_s \varphi(x,s))ds \\
& =\int_s^T (v_2(x,s)\cdot Df(x,s),\varphi(x,s))ds
\end{aligned}
$$

因此, $v_2$ 满足:

$$
\begin{aligned}
& (v_2(x,t),\varphi(x,t)) \\
& \leq (g(x),\varphi(x,T))+\int_t^T (l(x,s,\alpha),\varphi(x,s))ds \\
\end{aligned}
$$

以及对于 $\forall \varepsilon>0$, 存在 $\alpha'$ s.t.

$$
\begin{aligned}
& (v_2(x,t),\varphi(x,t))-\varepsilon \\
& \geq (g(x),\varphi(x,T))+\int_t^T (l(x,s,\alpha'),\varphi(x,s))ds \\
\end{aligned}
$$

由于 $\phi$ 是任意的，我们有

$$ v_2(x,t)\leq g(x)+\int_t^T l(x,s,\alpha) ds $$

以及

$$ v_2(x,t)-\varepsilon\geq g(x)+\int_t^T l(x,s,\alpha') ds $$

结合以上两个不等式，我们最终得到

$$ v_2(x,t)=\sup_{\alpha} { \int_t^T l(x,s,\alpha)ds+g(x) }=\sup_{\alpha} J(\alpha) $$

由于上确界是唯一的, 则 $v_1=v_2$, i.e. HJB方程的弱解是唯一的.

Numerical method to solve HJB equation

最优控制问题和其对应的HJB方程通常与现实问题相联系. 在这种情况下，我们可能会想知道解看上去怎么样. 适用于一般的PDE的数值方法，例如finite difference method 和 discountinuous Galerkin method，可能无法用于HJB方程. 因此，建立特别的算法，同时保证效率和精确度，是重要的. 其中一种方法是Hierarchical Dirichlet process (HDP) algorithm [4].

我们首先离散化时间，并将最优控制问题重写为如下形式：

$$ x_{k+1}=f(x_k)+g(x_k)u(x_k) $$

伴随着 cost function

$$
\begin{aligned}
V(x_k) & =\sum_{n=k}^\infty Q(x_n)+u^T(x_n)Ru(x_n) \\
& =x_k^T Q x_k +u_k^TRu_k+V(x_{k+1})
\end{aligned}
$$

则, HJB 方程变为

$$ V(x_k)=\min_{u_k}(x_k^T Qx_k+u_k^T Ru_k+V(x_{k+1})) $$

我们用一个初始值$V_0(x)$ (通常 $=0$)开始HDP算法，然后我们可以通过求解以下方程得到$u_i,V_i$

$$
\begin{aligned}
u_i(x_k) & =\arg\min_{u}(x_k^TQx_k+uTRu+V_i(x_{k+1})) \\
& = \arg\min_{u}(x_k^TQx_k+uTRu+V_i(f(x_k)+g(x_k)u)) \\
& = \frac{1}{2}R^{-1}g(x_k)T \frac{\partial V_i(x_{k+1})}{\partial x_{k+1}}
\end{aligned}
$$

以及

$$
\begin{aligned}
V_{i+1}(x_k) & =\min_{u}(x_k^TQx_k+uTRu+V_i(x_{k+1})) \\
& =x_k^TQx_k+u_iT(x_k)Ru_i(x_k) \\
& \quad +V_i(f(x_k)+g(x_k)u_i(x_k))
\end{aligned}
$$

对于 $i\geq 0$.

我们将展示通过HDP算法得到的$\{V_i\}$ 收敛至HJB方程的解.

Lemma 3.1: 设 $\mu_i$ 为任意一列 controls, 并定义 $\Lambda_i$

$$ \Lambda_{i+1}(x_k)=Q(x_k)+\mu_i^T R\mu_i +\Lambda_i (x_{k+1}) $$

If $V_0(x_k)=\Lambda(x_k)=0$, then $V_i(x_k)\leq \Lambda_i(x_k)$ 对于 $i\geq 0$.

Lemma 3.2: 若原始的最优控制问题是controllable的, 则

1. 存在一个上界 $Y(x_k)$ 对于 $V_i(x_k)$
2. 若HJB方程可解, 则上界可达到上确界, 记为 $V^*(x_k)$, 为HJB方程的解.

Theorem: If $V_0(x_k)=0$, then $\{V_i\}$ 是单调不减的，并且收敛至 $V^*$.

Proof:
设 $\mu_i(x_k)=u_{i+1}(x_k)$ 并定义 $\Lambda_i$

$$ \Lambda_{i+1}(x_k)=Q(x_k)+u_{i+1}^TRu_{i+1}+\Lambda_i(x_{k+1}) $$

由Lemma 3.1, 我们有 $V_i(x_k)\leq \Lambda_i(x_k)$ 对任意的 $i\geq 0$. 我们将通过归纳法证明 $V_{i+1}(x_k)\geq \Lambda_i(x_k)$.

对于 $i=1$, 我们有

$$ V_1(x_k)-\Lambda_0(x_k)=Q(x_k)\geq 0 $$

i.e. $V_1(x_k)\geq \Lambda_0(x_k)$. 对于 $i\geq 1$, 假设$V_i(x_k)\geq \Lambda_{i-1}(x_k)$ 成立, 则我们有

$$ V_{i+1}(x_k)-\Lambda_i(x_k)=V_i(x_{k+1})-\Lambda_{i-1}(x_{k+1})\geq 0 $$

这意味着 $V_{i+1}(x_k)\geq \Lambda_i(x_k)$. 因此, $V_{i}(x_k)$ 是单调不减的.

由Lemma 3.2 我们可知 $\{V_i(x_k)\}$ 有界. 因为它也是单调不减的, 则存在一个极限 $V_{\infty}$ 且

$$ \lim_{i\to\infty}V_i=V_{\infty} $$

因为 $V^*$ 是上确界, 我们有

$$ V_{\infty}\leq V^* $$

我们只需说明$V_{\infty}\geq V^*$. 由$V_i$的构造我们可得

$$
\begin{aligned}
& \quad V_\infty(x_k)=x_k^{TQx_k+u_\infty}T(x_k)Ru_\infty(x_k)+V_\infty(x_{k+1}) \\
& \Rightarrow V_\infty(x_{k+1})- V_\infty(x_k)=-x_k^{TQx_k+u_\infty}T(x_k)Ru_\infty(x_k) \\
\end{aligned}
$$

因此, $V_\infty(x_k)=Y(x_k)$. 由于 $V^*(x_k)$ 是最小上界, $V_\infty(x_k) \geq V^*(x_k)$. 于是,

$$ V_\infty(x_k)=V*^(x_k) $$

这意味着 $V_i$ 收敛至HJB方程的解.
□

Application

考虑一个简单的问题：我们希望一个在$x=10$的速度为0的车移动至$x=0$的时候速度也为零，并用时最少. 加速度的范围为$[-1,1]$. 设$u(t)$为车的位置，$v(t)$为速度，$\alpha(t)$为加速度. 我们的目的是求解如下最优控制问题：

$$
\left\{
\begin{aligned}
& \dot{x}(t)=\begin{pmatrix}
0 & 1 \\
0 & 0
\end{pmatrix}
x(t)+\begin{pmatrix}
0 \\
1
\end{pmatrix}
\alpha(t) \\
& x(0)=\begin{pmatrix}
10 \\
0
\end{pmatrix}
\end{aligned}
\right.
$$

其中 $x(t)=(u(t),v(t))^T$. cost function 为

$$ J(\alpha)=T=\int_0^T 1dt $$

我们首先需要求出对应的HJB方程. 定义value function $V(u,v)$

$$ V(u,v)=\inf_{\alpha\in [-1,1]}J(\alpha)=\inf_{\alpha\in [-1,1]}T_\alpha $$

这意味着从$(0,0)$ 到 $(u,v)$所用的最少时间. 因为$V(u,v)$不依赖于$t$，则HJB方程变为：

$$ \min_{\alpha\in[-1,1]} \{ f\cdot DV +1 \}=0 $$

其中 $f=(v,\alpha)^T$. 利用HDP algorithm, 我们可以得到$V(u,v)$的数值解：

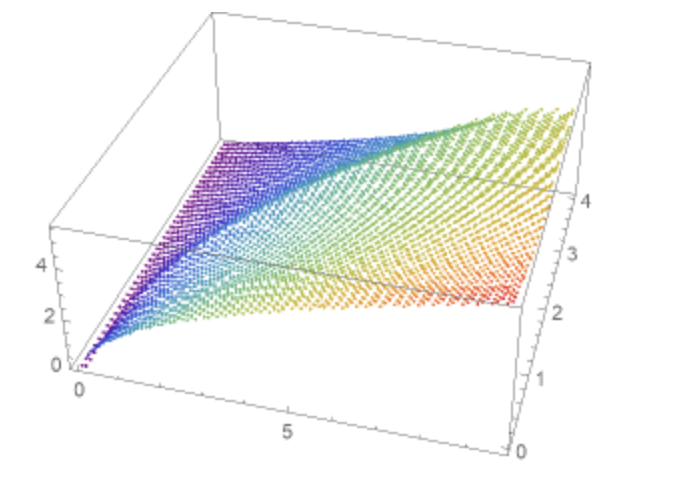
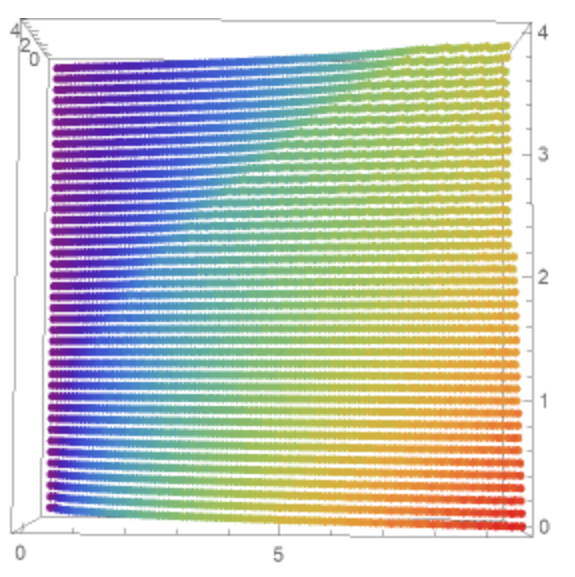
更进一步, 我们可以得到$u(t),v(t),\alpha(t)$的数值解：

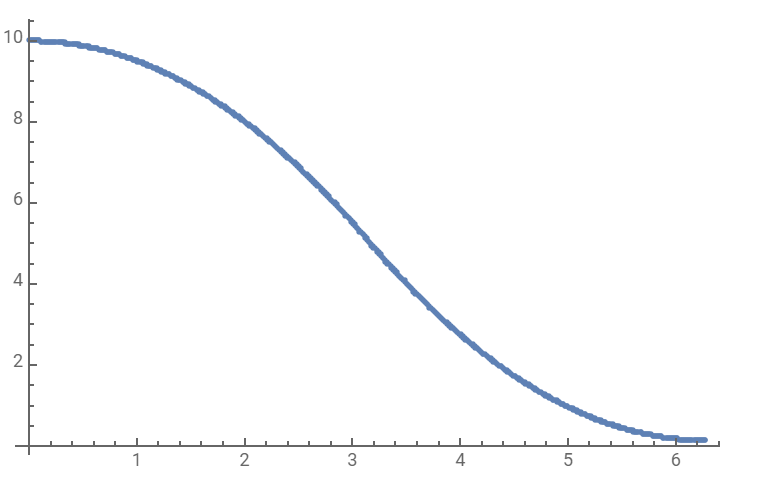
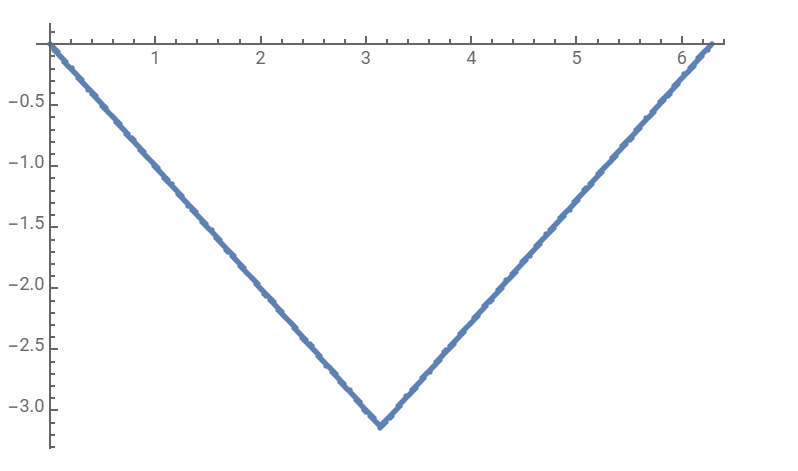
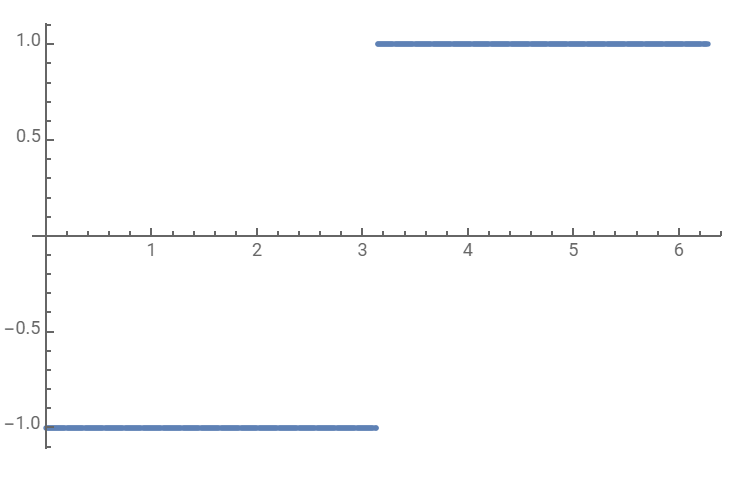
注意到加速度不是连续的. 在传统的微分方程数值解中，我们需要假设未知函数是连续的或者足够光滑的. 这个例子说明传统的数值方法可能不适用于最优控制问题. 因此，将原始问题转化为非线性HJB方程是一个有效的求解最优控制问题的方法.

Conclusion

我们已经展示了HJB方程的推导以及关于它的解的讨论. HJB方程在许多领域中有着重要的作用，例如物理或者经济. 求解最优控制问题仍然是研究的一个热点. 许多研究者正尝试将其于神经网络和深度学习相结合. 然而，维数灾难(curse of dimensionality)仍然是一个重要的问题. 尽管HDP算法在简单的小车问题中表现得十分良好，但当我们尝试解决高维问题时，计算所用的时间可能会超出可接受的范围. 一个可行的尝试为建立从高维到低维的映射，这通常会损失一定的精度. 另外的尝试是利用entropy method构造算法，这通常具有很好的收敛性质.

References

1. Lawrence Craig Evans, An Introduction to Mathematical Optimal Control Theory.
2. J. Yong, X. Y. Zhou, Stochastic Control, Hamilton Systems and HJB Equations, Appl. Math., 43, Springer-Verlag, New York, 1999.
3. WEI, L., WU, Z. and ZHAO, H., 2014. Sobolev weak solutions of the Hamilton Jacobi Bellman equations. SIAM Journal on Control and Optimization, 52 (3), pp. 1499 - 1526
4. Asma Al-Tamimi, Frank L. Lewis, and Murad Abu-Khalaf, Discrete-Time Nonlinear HJB Solution Using Approximate Dynamic Programming: Convergence Proof, IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS—PART B: CYBERNETICS, VOL. 38, NO. 4, AUGUST 2008
5. Y. Ouknine, I. Turpin, Weak solutions of semilinear PDEs in sobolev spaces and their probabilistic interpretation via the FBSDEs. Stochastic Analysis and Applications, 24 (2006), pp. 871-888.